Bevezetlés a DSP rejtelmeibe I.

Ebben a cikksorozatban szeretnék bemutatni néhány alapvető dolgot a digitális jelfeldolgozáshoz, minnél egyszerűbben és letisztultan, csak annyi matematikát használva, amennyi elengedhetetlen. Az első részben a szinuszjel előállításával és a legegyszerűbb modulációval ismerkedünk meg.

Szinuszjel generálás

Az egyszerűség kedvéért VBA-ban is megírtam jó néhány kódot, a könnyebb vizualizálás végett, és mert excelt mindenki használ, talán könnyebb végig menni a példakódokon és megérteni hogyan működik.

A legegyszerűbb mód szinusz jelet generálni a következő képpen lehet:

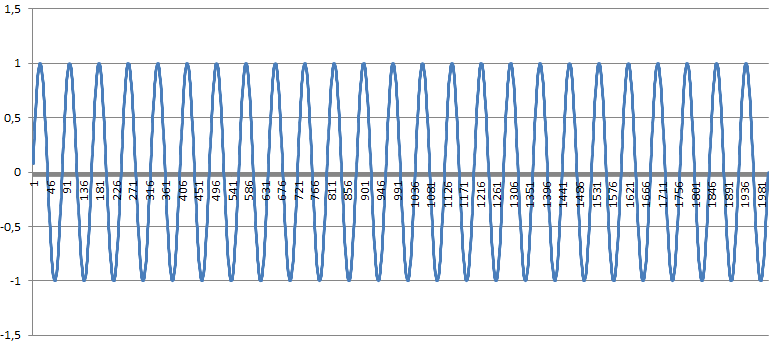
Sample[n] = Sin(2 * π * n * Frequency / SampleRate)

Az ebből eredő VBA kód:

Sub SinGen()
Application.Calculation = xlCalculationManual
Application.ScreenUpdating = False

Dim n, Freq, SampleRate, Amplitude As Integer

Freq = 100
SampleRate = 8000
Amplitude = 1
For n = 1 To 8000 Step 1 
    Cells(n, 1).Value = Amplitude * Sin((2 * WorksheetFunction.Pi * n * Freq / SampleRate))
    DoEvents 
Next n 
Application.Calculation = xlCalculationAuto
Application.ScreenUpdating = True
End Sub

A végeredmény pedig grafikonon ábrázolva:

C-ben a kód megírva így fest:

for (i = 0; i < 128; i++)
{
    sinBuffer[i] = (int)(100.0f * sin( 2.0f * 3.14159265358979323846f * 1600.0f * i / 20000.0f));
}

Mikrokontrollereken viszont sok erőforrást igényel a lebegőpontos számítás FPU nélkül. Ezért nézzük meg hogyan lehet gyorsaság szempontjából optimálisabban megoldani a feladatot.

Fixed pontos szinuszjel generálás táblázatos módszerrel

A táblázatos módszer lényege, hogy előre legeneráljuk a szinusz koefficienseket egy tömbbe, majd kiszámoljuk a sorszámát a soron következő mintának. Előnye, hogy jóval kevesebb számolást igényel, hátránya hogy kevésbé pontos. A pontosságot nagyban befolyásolja a használt táblázat mérete. Lebegőpontos számítás helyett frakcionális számítást használunk Q8.16 formátumban.

A teljes c kód:

#include <math.h>

#define PI 3.14159265358979323846f
#define TABLESIZE 256
#define SAMPLERATE 20000
#define FREQUENCY 2700
int16_t SinTable[TABLESIZE + 1];
uint32_t PhaseIncrement;
uint32_t PhaseAccumulator = 0;
uint32_t Fractional = 0;
uint32_t Index;
int16_t v1;
int16_t v2;
uint32_t result;
void InitSinTable()
{
 int i;
 for (i = 0; i < TABLESIZE + 1; i++)
 {
     SinTable[i] = (int16_t)(511.0f * sin(2.0f * PI * i / TABLESIZE));
 }
PhaseIncrement = 65536LL * TABLESIZE * FREQUENCY / SAMPLERATE;
}

uint16_t GetSinWave()
{
 PhaseAccumulator+=PhaseIncrement;
 PhaseAccumulator &= 0xFFFFFF;
 Index = PhaseAccumulator >> 16;
 Fractional = PhaseAccumulator & 0xFFFF;
 v1 = SinTable[Index];
 v2 = SinTable[Index + 1];
 result = v1 + (((v2 - v1) *  Fractional) >> 16);
 v1 = 0;
 return (uint16_t)(result);
}

A kód működése: egy tömbbe kiszámoljuk a sin(x)-et az előző módon megismert képlettel (csak most kihagyjuk a frekvenciát a képletből) , majd kiszámoljuk a kívánt frekvenciához tartozó index növelésének mértékét.  A PhaseAccumulátor Q8.16 formátumú frakcionális szám 16-24 bitje tartalmazza a tömbünk sorszámát. Végül lineáris interpolációval kiszámoljuk a soron következő minta értékét.

AM Moduláció

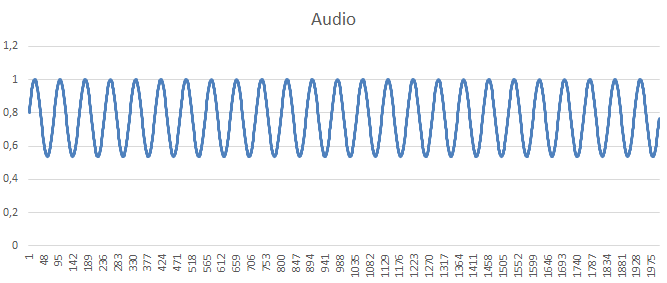
Miután megismerkedtünk a szinuszjel generálással, következzen a legegyszerűbb és legrégebbi moduláció. A fentiek alapján előállítjuk a vivőfrekvenciát, majd a modulálandó jellel összeszorozzuk. De mielőtt még megtennénk, a modulálandó jelet a modulációs mélységnek megfelelően „lehalkítjuk”, és DC offseteljük. A példában a modulálandó jel egy 100Hz-es szinuszhullám, a modulációs mélység pedig 30%.

VBA kód:

Sub GenAudio()

Dim Freq As Integer
Dim Ma As Double 'Modulation Amplitude
Dim Mi As Double 'Modulation percentage
Dim A As Double 'Calculated amplitude

Mi = 30
Freq = 100

Ma = 1 / ((100 / Mi) + 1)
A = Ma * 100 / Mi
For n = 1 To 8000 Step 1
Cells(n, 2).Value = A + (Ma * Sin(2 * WorksheetFunction.Pi * n * Freq / SampleRate))
DoEvents
Next n

End Sub

A kódot lefuttatva a következő jelet kapjuk:

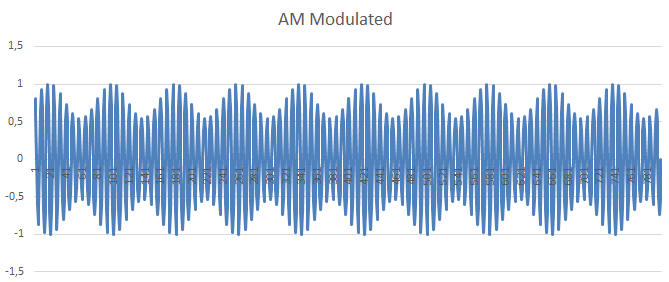
Ez után tehát jön a szorzás, amelynek során egy 1kHz-s szinuszjelet használtam a vivőfrekvenciának:

Sub Modulation()
For n = 2 To 8002 Step 1
    Cells(n, 3).Value = Cells(n, 1).Value * Cells(n, 2).Value
    DoEvents
Next n
End Sub

A végeredmény pedig:

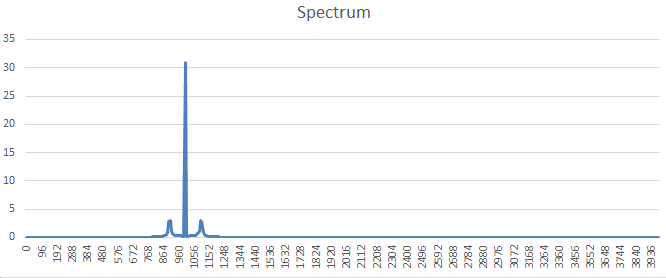
Az AM moduláció valójában frekvencia mixelés, amiről a következő fejezetek valamelyikében még bővebben kitérek. A mixelésből adódik hogy megjelenik a felső és alsó keverés is a kimeneten, ezért a sávszélesség kétszerese a legnagyobb átvitt frekvenciának. Jelen esetben a 100Hz-nek, ami szépen látszik a jel spektrumán:

Az AM modulációhoz a VBA kódot tartalmazhót excel itt letölthető és kipróbálható.